Introduction: The Role of PID in Feedback Control Systems
Proportional-Integral-Derivative (PID) controllers are among the most widely used control systems in engineering today. They are especially effective in single-input, single-output (SISO) applications where continuous feedback is required to maintain a desired output.
Given a plant process P that maps control actuator to system action
, select
so that
achieves a reference value
.
A classic example is the basic cruise control system you might find on your car. The control input signal is from the vehicle’s speed from the speedometer. The control output signal is the throttle position. From time to time, the car may encounter hills or other disturbances that necessitate a time-varying throttle output to maintain the speed reference.
Extending the Problem: Constrained SISO Systems
Given a plant process P, and system actions and
, select an single control actuator output
so that
achieves a reference value
subject to the constraint that
.
For example, maybe your car is actually a racecar, and there’s a torque limit on the tires that the engine should not exceed. In that case, the cruise control system needs to take the torque into account when setting the throttle, and there may be some situations, such as during an initial acceleration, when a normal SISO control loop wants to select throttles that would make the car exceed the torque specification.
In such a constrained-SISO problem there are three possible operating environments:
- The
limitation is not a factor:
. In that case, we want the controller to perform like a pure SISO controller on
.
- The
limitation dominates the controller, so that it is not possible to get close to
. In that case, we want the controller to perform like a pure SISO controller on
, with
.
- In transitions between these two regimes, we want a smooth hand-off from the dynamics of one controller to the other.
In such a constrained-SISO problem there is a natural inclination to want to use PID feedback control to handle both stages. After all, PID is intuitive and ubiquitous in industry. The question is: How do you combine two feedback loops that both have control of only a single output signal? Many common approaches to the “merge problem” result in undesirable modal behaviors—where there are abrupt transients “handing off” from one loop to the other.
One Solution Approach
Here is one solution, that unfortunately I cannot take credit for:
The intuition here is as follows: We want to control the signal, so create PID feedback loop on
. Most real PID controllers already have output saturation—that is, the output actuator is clipped at limits determined by the physical system[1]. To implement the constraint on
, we simply lower the upper control limit on the main PID loop when necessary to keep
at
.
But what is the upper limit on that makes
? The simple answer is that if we ever get the system into a state where
, and the control output happens to be
, then we have found limit. We declare that the limit output is either above or below whatever the current output is, in proportion to how close
is to the
. This estimate of the limit will be inaccurate when the controller is operating far away from the
condition, but it can be expected to become more and more accurate as
approaches
.
First Solution Analysis
Looking back at Figure 1, there is an algebraic loop, where the output signal feeds back to compute
.
Like any good Simulink problem, we can resolve this by adding a one-frame delay block to break the loop, and it turns out that this is the key to why this solution works.
To see why, let’s work out what an actual discrete-time controller is doing here[2]. The output saturation block works like this,
And the limit output is computed as
After some algebra we arrive at the following two conclusions.
| When the main loop dominates the limiter loop… | When the limiter loop dominates the main loop… |
From this, we can see that the limiter loop has the form of a rate limit, where the rate limit is proportional to the
error. If
overshoots
, the limiter even forces
to retreat at a minimum slew rate, regardless of the main loop error[3].
We can also use this result to analyze the controller in the continuous-time Laplace domain. When the limiter loop is dominating the main loop, we have
And after taking the Laplace transform (neglecting the constant):
Which rearranges to,
This has the form of an integral-only (I) controller, where the gain we specified is scaled by
.
But integral-only control is not appropriate for many plant systems. Can we operate a PI controller instead?
To do so, we want to modify the transfer function so that it reads:
But from the block diagram, above we need a signal that is related to the output signal by
. The Laplace transform of that equation gives
Neglecting the term, we can rearrange to show that
,
So
So to run PI control on the limiting signal using the intuitive scheme we selected, we need to compute an instantaneous derivative. For many systems this is not practical to achieve—if you want to compute the derivative of the input signal, you need a filter or compensator to estimate the derivative, and this introduces additional poles and zeros to the controller.
We can also reach a more general conclusion from all these Laplace transforms: The effect of breaking the algebraic loop using a delay is to apply one integrator to all control terms. Derivative terms become proportional terms; proportional terms become integral terms; and integral terms would become double-integral terms.
Can we redraw the block diagram so that we can have PI control on the  signal in the limiting case, without computing a derivative?
signal in the limiting case, without computing a derivative?
Let’s try it. The simplest, naïve way to get PI control on the main signal and have a different PI control on the
signal is simply to run two PI controllers and take the minimum output signal[4].
The question is: Does the merge using a min operation introduce undesirable modal switching behavior? That is, when we’re handing off from one loop to the other, do we get sudden and abrupt changes in the output signal?
To analyze this let’s look at the specific case where the main loop is the minimum loop on frame
, but the limiter
loop is the minimum on the very next control frame,
.
On the first frame, the control output is given by
Meanwhile, on the next frame the control output is given by
Now recall the same scenario with the original rate-limiting control scheme. In the same situation where the limit takes control on frame
, we had
We can line up these two equations. Remember that on the second equation we effectively have and
. After remembering that, we can find the necessary condition to ensure smooth control hand-off:
That is, the integrator state for the loop must match up with what the main
was doing on the previous frame. Here’s a detail on how that might work.
Instead of computing the absolute for each PI loop, we are computing the change requested by each:
.
Notice that this is again equivalent to computing the derivative of the input signal. In particular the term on each loop is now
. We have fundamentally failed in our goal of not computing a derivative!
However, we do get one major benefit from implementing the discrete-time controller in this manner. The “derivatives” that we do compute are pre-scaled by the discrete time period and by the gains into control output units. This form of computation minimizes the loss of numerical precision.
In Conclusion…
Engineering teams, including Sparx Engineering, continue to select PID controllers to solve control problems because they are easy to use, intuitive to design, and they work well on a wide variety of problems.
In this post, we looked at two non-linear extensions to the PID architecture to solve the constrained single-loop control problem. This is a common situation that Sparx has had to deal with in diverse problem domains. In both extensions, we found that individual P-, I-, and D- terms are effectively integrated one level into I-, II-, and P- terms. This effect can be compensated by differentiating all controller terms, but beware of complications that may arise from computing instantaneous derivatives.
[1] In the cruise control example, the throttle valve can never be more than 100% open or less than 0% open.
[2] For simplicity, I will set (turning PID into PI), I will implement integrators with Euler’s method, and I will gloss over other saturation limits, rate limits, and other elements that might be in a real control law.
[3] When , the term
becomes negative, representing a minimum negative slew rate, when
is configured for negative feedback.
[4] Once again, I am leaving out several features that would be in a real control law, like output saturation and anti-windup protection.
Featured Image Credit: https://benchmarkpdm.com/importance-of-shaft-alignment-parallel-angular-pump-alignment/
![Rendered by QuickLaTeX.com u[k+1] = \begin{cases} u_{\text{PID}}[k+1], & u_{\text{PID}}[k+1] \leq u_{\text{lim}}[k] \\ u_{\text{lim}}[k+1], & u_{\text{PID}}[k+1] > u_{\text{lim}}[k] \end{cases}](https://sparxeng.com/wp-content/ql-cache/quicklatex.com-c663c224d99c99931d06cde5015520a2_l3.png)
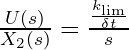
![Rendered by QuickLaTeX.com \begin{align*} I_{x_2}[k_0 + 1] &= I_{x_2}[k_0] + \delta t \cdot k_{i_{lim}}\left(x_2[k_0 + 1] - x_{2lim}\right) \\ u[k_0 + 1] = u_{x_2}[k_0 + 1] &= k_{p_{lim}}\left(x_2[k_0 + 1] - x_{2lim}\right) + I_{x_2}[k_0 + 1] \\ u[k_0 + 1] &= \left(k_{p_{lim}} + \delta t \cdot k_{i_{lim}}\right)\left(x_2[k_0 + 1] - x_{2lim}\right) + I_{x_2}[k_0]. \end{align*}](https://sparxeng.com/wp-content/ql-cache/quicklatex.com-6a9aa449b74062e9485799d57c74db4a_l3.png)